INTRODUCCIÓN
La teoría de la probabilidad es la parte de las matemáticas
que se encarga del estudio de los fenómenos o experimentos aleatorios. Por
experimento aleatorio entenderemos todo aquel experimento que cuando se le
repite bajo las mismas condiciones iniciales, el resultado que se obtiene no
siempre es el mismo. El ejemplo más sencillo y cotidiano de un experimento
aleatorio es el de lanzar una moneda o un dado, y aunque estos experimentos
pueden parecer muy modestos, hay situaciones en donde se utilizan para tomar
decisiones de cierta importancia.
para
diseñar, planear, recolectar, capturar, organizar, presentar, procesar y
analizar los datos obtenidos al realizar varios ensayos repetidos de un
experimento y para inferir conclusiones acerca de este último. Proporciona,
además, los métodos para el diseño estadístico de experimentos y para tomar
decisiones cuando aparecen situaciones de incertidumbre. Algunos autores
establecen que la estadística no es ciencia ya que algunas de las reglas que
emplea son empíricas.
En
esta investigación también se pretende hablar acerca del origen que ha tenido
la probabilidad estadística, así como también conocer más afondo las
habilidades que tiene y ver que otros usos tales como otras aplicaciones se le puede dar en nuestra vida
diaria
HISTORIA DE LA PROBABILIDAD
La historia de la
probabilidad comienza en el siglo XVII cuando Pierre Fermat » y Blaise Pascal » tratan de resolver algunos problemas
relacionados con los juegos de azar. Aunque algunos marcan sus inicios cuando
Cardano (jugador donde los haya) escribió sobre 1520 El Libro de los
Juegos de Azar (aunque no fue publicado hasta más de un siglo después,
sobre 1660) no es hasta dicha fecha que comienza a elaborarse una teoría
aceptable sobre los juegos.
Christian Huygens
conoció la correspondencia entre Blaise Pascal y Pierre Fermat suscitada por el
caballero De Meré, se planteó el debate de determinar la probabilidad de ganar
una partida, y publicó (en 1657) el primer libro sobre probabilidad: De
Ratiociniis in Ludo Aleae, (Calculating in Games of Chance), un tratado sobre
juegos de azar. Se aceptaba como intuitivo el concepto de equiprobabilidad, se
admitía que la probabilidad de conseguir un acontecimiento fuese igual al
cociente entre
Durante el siglo
XVIII, debido muy particularmente a la popularidad de los juegos de azar, el
cálculo de probabilidades tuvo un notable desarrollo sobre la base de la
anterior definición de probabilidad. Destacan en 1713 el teorema de Bernoulli y
la distribución binomial, y en 1738 el primer caso particular estudiado por De Moivre » , del teorema central del límite. En 1809 Gauss » inició el estudio de la teoría de errores y en
1810 Laplace, que había considerado anteriormente el tema, completó el
desarrollo de esta teoría. En 1812 Pierre Laplace » publicó Théorie analytique des
probabilités en el que expone un análisis matemático sobre los juegos de azar.
DEFINICIÓN DE PROBABILIDAD
- medida de la certidumbre que se le asocia a la ocurrencia u observación de un fenómeno o al hecho de que una característica de interés tome cierto valor.
- Mide la frecuencia con que se obtiene un resultado bajo condiciones suficientemente estables.
TIPOS DE PROBABILIDAD
- Probabilidad a priori: aquí la probabilidad de éxito se basa en el conocimiento anterior al proceso involucrado.
- Probabilidad clásica empírica: aunque la probabilidad se siga definiendo como la proporción entre el número de resultados favorables y el número de resultados, estos datos se basan en hechos observados no en el conocimiento anterior a un proceso.
- Probabilidad subjetiva: mientras que en los dos anteriores enfoques la probabilidad de un evento favorable se calcula objetivamente, ya fuera de un conocimiento previo o de datos reales y la probabilidad subjetiva se refiere a la posibilidad de ocurrencia asignada a un evento por un individuo particular.
• Probabilidad axiomática
(función matemática)
TIPOS DE EVENTOS
- Eventos elemental: A cada elemento o resultado posible del espacio muestral, se le conoce con el nombre de evento elemental.
- Eventos imposible: Algunos eventos nunca pueden ocurrir en el experimento aleatorio, y por eso se llama imposible. Se simboliza con Ø.
- Eventos seguro: Los eventos que siempre suceden en el experimento aleatorio, son llamados eventos seguros.
- Eventos complementario: Cuando se considera un evento A, el evento que contiene todos los eventos elementales del espacio muestral que no estén en A se denominara Evento Complementario.
TIPOS DE MUESTREO
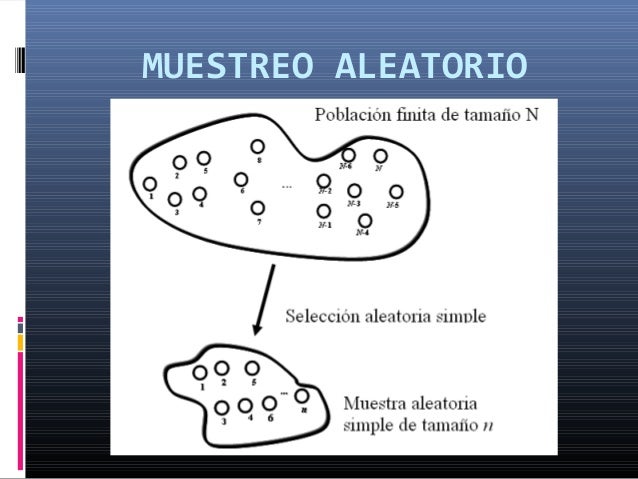
- Muestreo Aleatorio Simple: Cuando se selecciona un grupo de n unidades muéstrales de tal manera que cada muestra de tamaño n tenga la misma posibilidad de ser seleccionada.
- Muestreo Aleatorio Estratificado: Consiste en separar los elementos de la población en grupos que no presenten traslapes, llamados estratos, y la selección posterior de una muestra aleatoria simple de cada estrato.
- Muestreo Sistemático: Se obtiene al seleccionar aleatoriamente un elemento de los primeros k elementos en el marco y después seleccionar cada k-ésimo elemento a partir del primero.
- Muestreo por Conglomerados: Cuando cada unidad de muestreo aleatorio es a su vez una colección o conglomerado de elementos. En Geología se dice que un conglomerado es una colección de arenas de diferente tamaño.
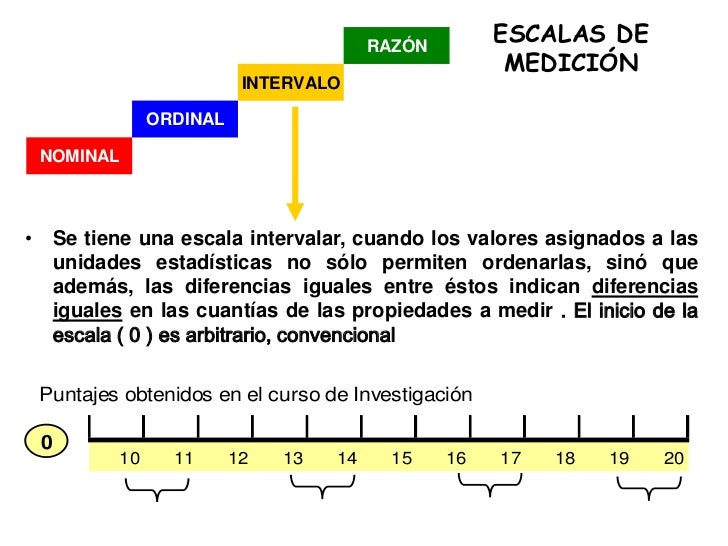
- Medición de Intervalo: La medición de intervalo posee las características de la medición nominal y ordinal. Establece la distancia entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto cero absoluto.
- Medición Nominal: En este nivel de medición se establecen categorías distintivas que no implican un orden específico. Por ejemplo, si la unidad de análisis es un grupo de personas, para clasificarlas se puede establecer la categoría sexo con dos niveles, masculino (M) y femenino (F), los respondientes solo tienen que señalar su género, no se requiere de un orden real. Así, si se asignan números a estos niveles solo sirven para identificación y puede ser indistinto: 1=M, 2=F o bien, se pueden invertir los números sin que afecte la medición: 1=F y 2=M.
- Medición Ordinal: Se establecen categorías con dos o más niveles que implican un orden inherente entre sí. La escala de medición ordinal es cuantitativa porque permite ordenar a los eventos en función de la mayor o menor posesión de un atributo o característica. Por ejemplo, en las instituciones escolares de nivel básico suelen formar por estatura a los estudiantes, se desarrolla un orden cuantitativo, pero no suministra medidas de los sujetos.
- Medición de Razón: Una escala de medición de razón incluye las características de los tres anteriores niveles de medición anteriores (nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría. Adicional mente tiene un punto cero absolutos, es decir, en el punto cero no existe la característica o atributo que se mide.
EJEMPLOS DE PROBABILIDAD
1. Se lanza al aire un dado normal (perfectamente equilibrado), enumere los posibles
resultados de este experimento.
Ω= {1, 2, 3, 4, 5, 6 }
2. Se lanza al aire dos veces una moneda normal, defina su espacio muestral.
Ω= {AA, AS, SA, SS}
b) Evento A.- El evento A es un subconjunto del espacio muestral.
AXIOMAS Y TEOREMAS
Para el cálculo de probabilidades hay que tomar en cuenta los Axiomas y Teoremas que a
continuación se enumeran.
1)La probabilidad de que ocurra un evento A cualquiera se encuentra entre cero y uno.
0 ≤ p(A) ≤1
2)La probabilidad de que ocurra el espacio muestral d debe de ser 1.
p(Ω) = 1
3)Si A y B son eventos mutuamente excluyentes, entonces la p(AUB) = p(A) + p(B)
Generalizando:
Si se tienen n eventos mutuamente excluyentes o exclusivos A1, A2, A3,.....An, entonces;
p(A1UA2U......... UAn) = p(A1) + p(A2) + .......+ p(An)
TEOREMA 1. Si φ es un evento nulo o vacío, entonces la probabilidad de que
ocurra φ debe ser cero.
p(φ)=0
TEOREMA 2. La probabilidad del complemento de A, Ac debe ser, p(Ac
)= 1 – p(A)
CONCLUSIÓN
a través de esta investigación pudimos darnos cuenta de que el contenido de esto nos lleva a obtener las probabilidades de posibles resultados como por ejemplo si lo relacionamos en nuestra carrera podremos crear un problema para saber que tanto probable es que siga aumentando el petroleo o que tanta probabilidad hay en que disminuya su producción, en la estadística se utiliza para muchas cosas al lanzar un dado o una moneda en nuestra vida diaria suceden muchas cosas que podemos resolver en base ala probabilidad o mejor dijo empleando el uso de la estadística, asiendo un muestreo en si empleando todos los conocimiento que hemos aprendido.
BIBLIOGRÁFICAS



No hay comentarios:
Publicar un comentario